反三角函数与简单三角方程
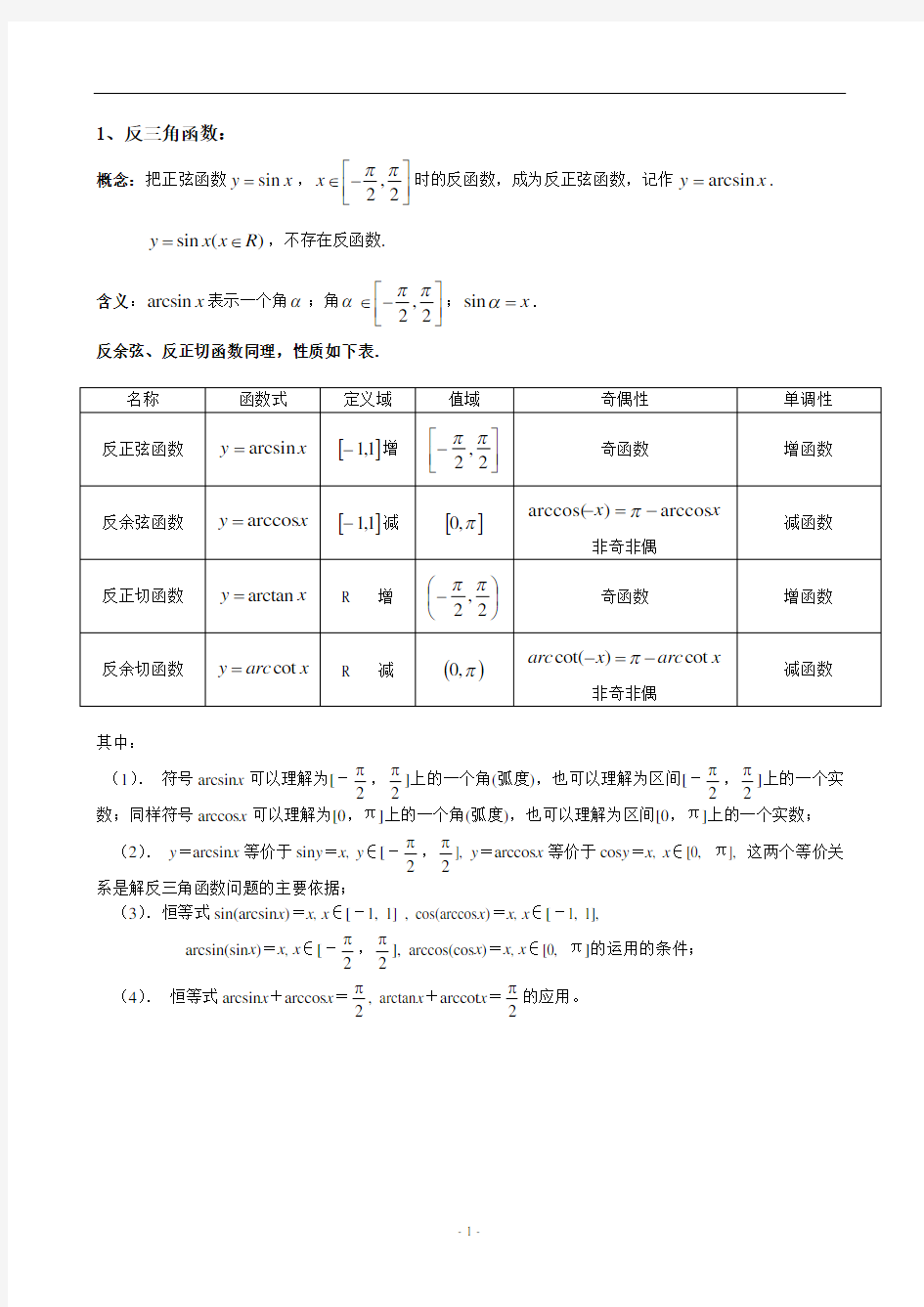

1、反三角函数:
概念:把正弦函数sin y x =,,22x ππ??
∈-
????
时的反函数,成为反正弦函数,记作x y arcsin =. sin ()y x x R =∈,不存在反函数.
含义:arcsin x 表示一个角α;角α,22ππ??
∈-????;sin x α=.
反余弦、反正切函数同理,性质如下表.
其中:
(1). 符号arcsin x 可以理解为[-
2π,2π]上的一个角(弧度),也可以理解为区间[-2π,2
π
]上的一个实数;同样符号arccos x 可以理解为[0,π]上的一个角(弧度),也可以理解为区间[0,π]上的一个实数; (2). y =arcsin x 等价于sin y =x , y ∈[-
2π,2
π
], y =arccos x 等价于cos y =x , x ∈[0, π], 这两个等价关系是解反三角函数问题的主要依据;
(3).恒等式sin(arcsin x )=x , x ∈[-1, 1] , cos(arccos x )=x , x ∈[-1, 1],
arcsin(sin x )=x , x ∈[-
2π,2π
], arccos(cos x )=x , x ∈[0, π]的运用的条件; (4). 恒等式arcsin x +arccos x =2π, arctan x +arccot x =2
π
的应用。
名称 函数式
定义域
值域
奇偶性 单调性 反正弦函数
x y arcsin =
[]1,1-增
??
????-2,2ππ 奇函数
增函数
反余弦函数
x y arccos =
[]1,1-减
[]π,0
x x arccos )arccos(-=-π
非奇非偶 减函数
反正切函数
arctan y x =
R 增
??
? ??-2,2ππ 奇函数
增函数
反余切函数 cot y arc x =
R 减
()π,0
cot()cot arc x arc x π-=-
非奇非偶
减函数
2、最简单的三角方程
方程 方程的解集
a x =sin
1=a {}Z k a k x x ∈+=,arcsin 2|π
1 (){}Z k a k x x k ∈-+=,arcsin 1|π a x =cos 1=a {}Z k a k x x ∈+=,arccos 2|π 1 {}Z k a k x x ∈±=,arccos 2|π tan x a = {}|arctan ,x x k a k Z π=+∈ cot x a = {}|cot ,x x k arc a k Z π=+∈ 其中: (1).含有未知数的三角函数的方程叫做三角方程。解三角方程就是确定三角方程是否有解,如果有解,求出三角方程的解集; (2).解最简单的三角方程是解简单的三角方程的基础,要在理解三角方程的基础上,熟练地写出最简单的三角方程的解; (3).要熟悉同名三角函数相等时角度之间的关系在解三角方程中的作用; 如:若sin sin αβ=,则sin (1)k k απβ=+-;若cos cos αβ=,则2k απβ=±; 若tan tan αβ=,则a k πβ=+;若cot cot αβ=,则a k πβ=+; (4).会用数形结合的思想和函数思想进行含有参数的三角方程的解的情况和讨论。 【例题精讲】 例1. 函数,,的反函数为( )y x x =∈??? ???sin π π2 32 []A y x x .a r c s i n =∈-,,11 [] B y x x .arcsin =-∈-,,11 [] C y x x .a r c s i n =+∈-π,,11 [] D y x x .arcsin =-∈-π,,11 分析与解: π π2 32 ≤≤ x ∴?-??????x x π π2 2,,需把角转化至主值区间。 ∴- ≤-≤ -==π ππ π2 2 x x x y ,又sin()sin 由反正弦函数定义,得π-=x y arcsin ∴=--≤≤x y y πa r c s i n ,又由已知得11 [] ∴=-∈-所求反函数为,,y x x πarcsin 11 例4. 函数,,的图象为()y x x =∈- ??????arccos(cos )π π2 2 π 2 π 2 -π 2 - π 2 O π 2 O π 2 - π 2 (A ) (B ) 1 1 - π 2 - π 2 O π 2 O π 2 -1 (C ) (D ) 分析与解: 解析式可化简为,,,,y x x x x x ==∈? ? ?? ?-∈-??????????? ??arccos(cos )0220ππ 即,,,,显然其图象应为()y x x x x A =∈? ? ?? ?-∈-???? ??????? ??0220ππ 例5. 函数,, 的值域为()y x x =∈- arccos(sin )()π π 3 23 A B ..π ππ656056,,?? ?? ?? ????? C D ..π ππ π3236 23,,?? ?? ??????? 分析与解: 欲求函数值域,需先求,, 的值域。u x x =∈- sin ()π π 3 23 - << ∴-<≤-<≤π π3 2332132 1x x u ,,即sin [] 而在,上为减函数y u =-arccos 11 ∴- >≥a r c c o s ()a r c c o s a r c c o s 3 2 1u 即,故选()056 ≤ 例6.使arcsin arccos x x >成立的x 的取值范围是( ) A B ..022221,,?? ? ?? ?? ? ?? [)C D ..-?? ?? ? ?-12210, , 分析与解: 该题研究不等关系,故需利用函数的单调性进行转化,又因为求x 的取值范围,故需把x 从反三角函数式中分离出来,为此只需对arcsinx ,arccosx 同时取某一三角函数即可,不妨选用正弦函数。 若,则,,而,x x x ≤∈- ??????∈???? ? ?0202arcsin arccos πππ 此时不成立,故arcsin arccos x x x >>0 若,则, ,,x x x >∈?? ? ??∈? ? ?? ?00202arcsin arccos ππ 而在区间, 上为增函数y x =? ? ? ? ?sin 02π 又a r c s i n a r c c o s s i n (a r c s i n )s i n (a r c c o s )x x x x >∴> 即,解不等式,得x x x >-> 12 2 2 || 又,故选()012 2 1<≤∴ <≤x x B 例7. []若,则()022<<+???? ? ?++=απ παπαarcsin cos()arccos sin() A B C D . .. .π π π απ α2 2 2 22 2- -- - 分析与解:这是三角函数的反三角运算,其方法是把角化到相应的反三角函数的值域内。 a r c s i n c o s ()a r c s i n (s i n )a r c s i n (s i n )π αααα2 +?? ??? ?=-=-=- []a r c c o s s i n ()a r c c o s (s i n )a r c c o s (s i n )πααπα+=-=- =--? ? ??? ?=--= +ππ αππ απ αa r c c o s c o s ()( ),2 2 2 ∴=-++= 原式,故选()()( )απ απ 2 2 A 例8. 求值:(1)3sin 2arcsin 5????- ??????? (2)1 1tan arccos 2 3?? ??? 分析:arcsin()arcsin()sin -- ??????=-3 5 2 235表示,上的角,若设,则易得π παα =-3 5 2,原题即是求的值,这就转化为早已熟悉的三角求值问题,解决此类sin α问题的关键 是能认清三角式的含义及运算次序,利用换元思想转化为三角求值。 解:()设,则13535 arcsin()sin -==- αα αππαα∈-???? ??∴=-=2 214 52,,cos sin ∴==?-?=-s i n s i n cos ()()2223 5452425 ααα 即s i n a r c s i n ()2352425 -?? ??? ?=- ()设,则21313 arccos cos ==αα [] απ αα∈∴=-= 0122 3 2,s i n cos ∴=-=- =tg ααα2111 3223 22cos sin 即tg 121322arccos ????? ?= 例9.知函数2()arccos()f x x x =- (1)求函数的定义域、值域和单调区间;(2)解不等式:()(21)f x f x <+ 解:(1)由112 ≤-≤-x x 得 2 51251+≤ ≤-x 又]1,41[41)21(22 -∈--=-x x x ∴)(x f 的定义域为]2 5 1,251[ +-,值域为]41arccos ,0[-π 又∵]2 1 ,251[ -∈x 时,x x x g -=2)(单调递减,x y arccos =单调递减,从而)(x f 递增 ∴)(x f 的单调递增区间是]21,251[-,同理)(x f 的单调递减区间是]2 5 1,21[+ ( 2 ) )]2 1 2()212arccos[()arccos()212()(22+-+<-+ 即)4 14arccos()arccos(2 2-<-x x x ∴??? ? ? ? ??? ->-≤-≤-≤-≤-41414141112 222x x x x x x 解不等式组得6121<<-x ∴不等式的解集为)61,21(- 简单的三角方程 例1.写出下列三角方程的解集 (1)2 sin()8 2 x π - = ; (2)2cos310x +=; (3)cot 3x = 解集{x|x=(k π+arctg3)2,k ∈Z} 例2.求方程tan(3)34 x π + =在[]0,2π上的解集. 说明 如何求在指定区间上的解集?(1)先求出通解,(2)让k 取适当的整数,一一求出在指定区间上的特解,(3)写指定区间上的解. 例3.解方程2 2sin 3cos 10x x ++= 解:方程化为22cos 3cos 30x x --= 说明 可化为关于某一三角函数的二次方程,然后按二次方程解. 例4. 解方程①3sin 2cos 0x x -= ②2 2 2sin 3sin cos 2cos 0x x x x --= ②除以cos 2x 化为2tg 2x-3tgx-2=0. 说明 关于sinx ,cosx 的齐次方程的解法:方程两边都除cos n x(n=1,2,3,…)(∵cosx=0不是方程的解),转化为关于tgx 的方程来解. 例5.解方程:(1)3sin 2cos21x x -= (2)5sin 312cos3 6.5x x -= 思考:引入辅助角,化为最简单的三角方程 2x-30°=k180°+(-1)k 30° ∴x=k90°+(-1)k15°+15°(k ∈Z)所以解集是 {x|x=k90°+(-1)k15°+15°,k ∈Z} 于是x=k60°+(-1)k 10°+22°38′,(k ∈Z) ∴原方程的解集为{x|x=k60°(-1)k 10°+22°38′,k ∈Z} 最简单的三角方程. 例6.解方程2 2sin 3cos 0x x +=. 解 原方程可化为 2 2(1c o s ) 3c o s 0 x x -+=, 即 2 2cos 3cos 20x x --=. 解这个关于cos x 的二次方程,得 cos 2x =,1 cos 2 x =-. 由cos 2x =,得解集为φ; 由1cos 2x =- ,得解集为22,3x x k k Z ππ??=±∈???? . 所以原方程的解集为22,3x x k k Z ππ?? =± ∈???? . [说明]方程中的2sin x 可化为2 1cos x -,这样原方程便可看成以cos x 为未知数的一元二次方程,当0 ?≥时,可用因式分解将原方程转化成两个最简方程,从而求得它们的解. 【拓展提高】 例1.若方程cos 22sin 10x x m -+-=存在实数解,求m 的取值范围. 解一 由原方程,得 22sin 2sin 0x x m +-=, 即 2 sin sin 02 m x x +- = 解这个以sin x 为未知数的一元二次方程,因为1sin 1x -≤≤ 要使方程有解,只需14()02 1102 m m ? ?=-?-≥????+-≥?? 解得1 42 m - ≤≤. 所以m 的取值范围为1,42?? - ???? . [说明] 有关三角方程的实数解问题,不仅要考虑以sin x 为未知数的一元二次方程的0?≥,而且必须考虑sin x 的值在 []1,1-内. 解二 由原方程得 2 2sin 2sin 0x x m +-=, 得22 112sin 2sin 2(sin )22 m x x x =+=+- 因为1sin 1x -≤≤,所以1 42 m -≤≤. 所以m 的取值范围为1,42?? - ???? . [说明] 当方程sin (x t t =为常数)有解时,必须满足1t ≤, 则原题就转化为求[]211 2(),1,122 m t t =+- ∈-的最大值、最小值问题. 例2.求方程sin 2cos()x x π=-的解集. 解一 由原方程得2sin cos cos x x x ?=-, 得 cos 0x =,1sin 2 x =- . 由cos 0x =,得解集为,2x x k k Z π π??=+ ∈??? ? ; 由1sin 2x =- ,得解集为(1),6K x x k k Z ππ??=--∈???? . 所以原方程的解集为(1),2 6K x x k x k k Z π π ππ?? =+ =--∈??? ? 或. 解二 由原方程得sin 2cos x x =-, 即3sin 2sin()2 x x π =+ 得3222x k x ππ=+ +或322()2x k x π ππ=+-+, 即322x k ππ=+或236 k x ππ = -,k Z ∈. 所以原方程的解集为322,236k x x k x k Z ππππ?? =+ =-∈???? 或. 解三 由原方程得sin 2cos x x =-, 即cos(2)cos 2 x x π += 得222 x k x π π+ =+或222 x k x π π+ =-, 即22 x k π π=- 或236 k x ππ = -,k Z ∈. 所以原方程的解集为22,2 36k x x k x k Z π πππ?? =- = -∈??? ? 或. [说明] 由于转化方法的不同,所得解集的表达形式不同,通过验证这些解集是相等的集合.对于两个相等 的同名三角函数所组成的三角方程,可直接利用以下关系得到方程的解. (1)sin sin αβ=,则2k απβ=+或2,k k Z αππβ=+-∈; (2)cos cos αβ=,则2k απβ=+或2,k k Z απβ=-∈; (3)tan tan αβ=,则,k k Z απβ=+∈. 【巩固练习】 反三角函数 1.3arctan(tan )5 π 的值是 ( ) A.35π- B. 25π C.25 π- D.35π 2.下列关系式中正确的是 ( ) A. 55cos cos 44arc ππ?? ??- =- ??? ???? B. sin arcsin 33ππ??= ??? C. cos cos cos cos 44arc arc ππ? ? ? ?= ? ?? ?? ? D.1tan(2)cot()2arc arc -=- 3.函数()arcsin(tan )f x x =的定义域是 ( ) A.,44ππ?? - ???? B.(),44k k k Z ππππ??-+∈???? C.(),(1)44k k k Z π πππ??+ +-∈??? ? D.()2,244k k k Z ππππ? ?-+∈??? ? 4.在31,2 ??-??? ? 上和函数y x =相同的函数是 ( ) A.arccos(cos )y x = B.arcsin(sin )y x = C.sin(arcsin )y x = D.cos(arccos )y x = 5.函数arctan 2 x y π=+的反函数是 . 6.求sin y x =在3,22ππ?? ???? 上的反函数. 7.比较5arccos 4??- ? ??? 与1cot()2arc -的大小. 51 arccos cot()42 arc ??->- ? ??? 8.研究函数() 2 arccos y x x =-的定义域、值域及单调性. 9.计算:45cos arccos arccos 513????-- ??????? 10.求下列函数的定义域和值域: (1) y =arccos x 1; (2) y =arcsin(-x 2+x ); (3) y =arccot(2x -1), 解:(1) y =arccos x 1, 0< x 1≤1, ∴ x ≥1, y ∈[0, 2 π). (2) y =arcsin(-x 2+x ), -1≤-x 2+x ≤1, ∴ 251-≤x ≤2 5 1+, 由于-x 2+1=-(x -21 )2+41, ∴ -1≤-x 2+x ≤41, ∴ -2 π≤y ≤arcsin 41. (3) y =arccot(2x -1), 由于2x -1>-1, ∴ 0< arccot(2x -1)<43π, ∴ x ∈R , y ∈(0, 4 3π ). 11.求函数y =(arccos x )2 -3arccos x 的最值及相应的x 的值。 解:函数y =(arccos x )2-3arccos x , x ∈[-1, 1], arccos x ∈[0, π] 设arccos x =t , 0≤t ≤π, ∴ y =t 2-3t =(t -23)2-4 9 , ∴ 当t =23时,即x =cos 23时, 函数取得最小值-4 9 , 当t =π时,即x =-1时,函数取得最大值π2 -3π. 简单的三角方程 1.解下列方程. (1)2 tan 1x = (2)sin 5sin 3x x = (2)5x=2k π+3x 或5x=2k π+π-3x x k π∴=或21 8 k x π+= ()k Z ∈ 2.方程sin2x =sin x 在区间(0, 2π)内的解的个数是 3个 . 解:作出函数y =sin2x 和y =sin x 的图象,由图象知,它们的交点有3个。 3.(1) 方程tan3x =tg x 的解集是{x | x =k π, k ∈Z }. (2) 方程sin x +cos x = 2 2 在区间[0, 4π]上的所有的解的和是 9π . x y O |D 2|D 4.解方程2223 sin sin cos cos 03 x x x x - -=. 解一 因为cos 0x ≠(使cos 0x =的x 的值不可能满足原方程),所以在方程的两边同除以2cos x ,得 223 tan tan 103 x x - -=. 解关于tan x 的二次方程,得 tan 3x =,3tan 3 x =- . 由tan 3x =,得解集为,3x x k k Z π π??=+ ∈??? ? ; 由3 tan 3x =- ,得解集为,6x x k k Z ππ??=-∈???? . 所以原方程的解集为,,3 6x x k x k k Z π π ππ?? =+ =- ∈??? ? 或. 三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1 cotAcotB -+ 倍角公式 tan2A = A tan 12tanA 2 - Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3 π -a) 半角公式 sin( 2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2 A )= A A cos 1cos 1-+ tan(2 A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cos b = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2 b a - tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB 积化和差 sinasinb = - 21[cos(a+b)-cos(a-b)] cosacosb = 2 1 [cos(a+b)+cos(a-b)] 三角、反三角函数图像 六个三角函数值在每个象限的符号: sinα·cscα cosα·secα tanα·cotα 三角函数的图像和性质: 1-1y=sinx -3π2 -5π2 -7π2 7π2 5π 2 3π2 π2 -π2 -4π-3π -2π4π 3π 2ππ -π o y x 1-1y=cosx -3π 2 -5π2 -7π 2 7π2 5π2 3π2 π2 -π2 -4π-3π-2π4π 3π 2π π -π o y x y=tanx 3π2 π π2 - 3π2 -π - π2 o y x y=cotx 3π2 π π2 2π -π - π2 o y x 函数 y=sinx y=cosx y=tanx y=cotx 定义域R R {x|x∈R且x≠kπ+ 2 π ,k∈Z} {x|x∈R且x≠kπ,k∈Z}值域 [-1,1]x=2kπ+ 2 π 时y max=1 x=2kπ- 2 π 时y min=-1 [-1,1] x=2kπ时y max=1 x=2kπ+π时y min=-1 R 无最大值 无最小值 R 无最大值 无最小值 周期性周期为2π周期为2π周期为π周期为π 奇偶性奇函数偶函数奇函数奇函数 单调性 在[2kπ- 2 π ,2kπ+ 2 π ]上都是增函数;在 [2kπ+ 2 π ,2kπ+ 3 2 π]上都是减函数(k∈Z) 在[2kπ-π,2kπ]上都是增函数; 在[2kπ,2kπ+π]上都是减函 数(k∈Z) 在(kπ- 2 π ,kπ+ 2 π )内都是增函数 (k∈Z) 在(kπ,kπ+π)内都是减函数 (k∈Z) 第二章 三角、反三角函数 一、考纲要求 1.理解任意角的概念、弧度的意义,能正确进行弧度和角度的互换。 2.掌握任意角的正弦、余弦、正切的定义,了解余切、正割、余割的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义。 3.掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式。 4.能正确运用三角公式,进行简单三角函数式的化简,求值和恒等式的证明。 5.了解正弦函数、余弦函数,正切函数的图像和性质,会用“五点法”画正弦函数,余弦函数和函数y=Asin(wx+?)的简图,理解A 、w 、?的物理意义。 6.会由已知三角函数值求角,并会用符号arcsinx 、arccosx 、arctgx 表示。 7.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决三角形的计算问题。 8.理解反三角函数的概念,能由反三角函数的图像得出反三角函数的性质,能运用反三角函数的定义、性质解决一些简单问题。 9.能够熟练地写出最简单的三角方程的解集。 二、知识结构 1.角的概念的推广: (1)定义:一条射线OA 由原来的位置OA ,绕着它的端点O 按一定方向旋转到另一位置OB ,就形成了角α。其中射线OA 叫角α的始边,射线OB 叫角α的终边,O 叫角α的顶点。 (2)正角、零角、负角:由始边的旋转方向而定。 (3)象限角:由角的终边所在位置确定。 第一象限角:2k π<α<2k π+2 π ,k ∈Z 第二象限角:2k π+ 2 π <α<2k π+π,k ∈Z 第三象限角:2k π+π<α<2k π+2 3π ,k ∈Z 第四象限角:2k π+2 3π <α<2k π+2π,k ∈Z (4)终边相同的角:一般地,所有与α角终边相同的角,连同α角在内(而且只有这样的角),可以表示为k 2360°+α,k ∈Z 。 (5)特殊角的集合: 终边在坐标轴上的角的集合{α|α= 2 π k ,k ∈Z } 终边在一、三象限角平分线上角的集合{α|α=k π+4π ,k ∈Z } 终边在二、四象限角平分线上角的集合{α|α=k π-4π ,k ∈Z } 终边在四个象限角平分线上角的集合{α|α=k π-4 π ,k ∈Z } 2.弧度制: (1)定义:用“弧度”做单位来度量角的制度,叫做弧度制。 (2)角度与弧度的互化: 1°= 180 π 弧度,1弧度=( π 180 )° (3)两个公式:(R 为圆弧半径,α为圆心角弧度数)。 弧长公式:l=|α|R 三角和反三角函数图像 The Standardization Office was revised on the afternoon of December 13, 2020 三角、反三角函数图像 六个三角函数值在每个象限的符号: sinα·cscα cosα·secα tanα·cotα 三角函数的图像和性质: 1-1y=sinx -3π2 -5π2 -7π2 7π2 5π 2 3π2 π2 -π2 -4π-3π -2π4π 3π 2ππ -π o y x 1-1y=cosx -3π 2 -5π2 -7π 2 7π2 5π2 3π2 π2 -π2 -4π-3π-2π4π 3π 2π π -π o y x y=tanx 3π2 π π2 - 3π2 -π - π2 o y x y=cotx 3π2 π π2 2π -π - π2 o y x 函数 y=sinx y=cosx y=tanx y=cotx 定义域 R R {x |x ∈R 且x≠kπ+ 2 π ,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z } 值域 [-1,1]x=2kπ+ 2 π 时y max =1 x=2kπ- 2 π 时y min =-1 [-1,1] x=2kπ时y max =1 x=2kπ+π时y min =-1 R 无最大值 无最小值 R 无最大值 无最小值 周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性 奇函数 偶函数 奇函数 奇函数 单调性 在[2kπ- 2π,2kπ+2 π ]上都是增函数;在[2kπ+2 π ,2kπ+32π]上都是减函数(k ∈Z) 在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k ∈Z) 在(kπ- 2π,kπ+2 π )内都是增函数(k ∈Z) 在(kπ,kπ+π)内都是减函数(k ∈Z) 三角、反三角函数 一、考纲要求 1.理解任意角的概念、弧度的意义,能正确进行弧度和角度的互换。 2.掌握任意角的正弦、余弦、正切的定义,了解余切、正割、余割的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义。 3.掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式。 4.能正确运用三角公式,进行简单三角函数式的化简,求值和恒等式的证明。 5.了解正弦函数、余弦函数,正切函数的图像和性质,会用“五点法”画正弦函数,余弦函数和函数y=Asin(wx+?)的简图,理解A 、w 、?的物理意义。 6.会由已知三角函数值求角,并会用符号arcsinx 、arccosx 、arcotx 表示。 7.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决三角形的计算问题。 8.理解反三角函数的概念,能由反三角函数的图像得出反三角函数的性质,能运用反三角函数的定义、性质解决一些简单问题。 9.能够熟练地写出最简单的三角方程的解集。 二、知识结构 1.角的概念的推广: (1)定义:一条射线OA 由原来的位置OA ,绕着它的端点O 按一定方向旋转到另一位置OB ,就形成了角α。其中射线OA 叫角α的始边,射线OB 叫角α的终边,O 叫角α的顶点。 (2)正角、零角、负角:由始边的旋转方向而定。 (3)象限角:由角的终边所在位置确定。 第一象限角:2k π<α<2k π+2 π ,k ∈Z 第二象限角:2k π+ 2 π <α<2k π+π,k ∈Z 第三象限角:2k π+π<α<2k π+2 3π ,k ∈Z 第四象限角:2k π+2 3π <α<2k π+2π,k ∈Z (4)终边相同的角:一般地,所有与α角终边相同的角,连同α角在内(而且只有这样的角),可以表示为k 2360°+α,k ∈Z 。 (5)特殊角的集合: 终边在坐标轴上的角的集合{α|α= 2 π k ,k ∈Z } 终边在一、三象限角平分线上角的集合{α|α=k π+4π ,k ∈Z } 终边在二、四象限角平分线上角的集合{α|α=k π-4π ,k ∈Z } 终边在四个象限角平分线上角的集合{α|α=k π-4 π ,k ∈Z } 2.弧度制: (1)定义:用“弧度”做单位来度量角的制度,叫做弧度制。 (2)角度与弧度的互化: 反三角函数公式 反三角函数图像与特征 1 : 反三角函数的定义域与主值范围 式中n为任意整数. 反三角函数的相互关系 sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞ If x > 0.5 And x <= 1 Then ArcSin = -Atn(Sqr(1 - x * x) / x) + 2 * Atn(1) End Function ArcCos(x) 函数 功能:返回一个指定数的反余弦值,以弧度表示,返回类型为Double。 语法:ArcCos(x)。 说明:其中,x的取值范围为[-1,1],x的数据类型为Double。 程序代码: Function ArcCos(x As Double) As Double If x >= -1 And x < -0.5 Then ArcCos = Atn(Sqr(1 - x *x) / x) + 4 * Atn(1) If x >= -0.5 And x <= 0.5 Then ArcCos = -Atn(x/ Sqr(1 - x * x)) + 2 * Atn(1) If x> 0.5 And x <= 1 Then ArcCos = Atn(Sqr(1 - x*x) / x) End Function §6.4.1 反三角函数(1)——反正弦函数 [教学过程] 一.反正弦函数的引入 1.回忆 sin y x =的图像及反函数的条件,可知sin ,y x x =∈R 不存在反函数 2.若,22x ππ??∈-????,则sin y x =是单调函数,,x y 一一对应,故在,22x ππ?? ∈-???? 上sin y x =存在反函数 3.定义 ()sin ,,22f x x x ππ?? =∈-???? ,其反函数()1arcsin f x x -=,称为反正弦函数 二.反正弦函数的图像 反函数的图像与原函数的图像关于y x =对称,即x 改y ,y 改x 三.根据解析式与图像研究反正弦函数的性质 sin ,,22y x x ππ?? =∈-???? []arcsin ,1,1y x x =∈- 1.值域 []1,1y ∈- ,22y ππ??∈-???? 2.奇偶性 奇函数(过原点) 奇函数(过原点) 3.单调性 增函数 增函数 4.周期性 非周期函数 非周期函数 5.()11arcsin sin arcsin 2 2 x x x x π π -≤≤?-≤≤ ?= 6.()1sin 1arcsin sin 2 2 x x x x π π -≤≤ ?-≤≤?= arcsin 是反正弦的 符号,是一个整体 数形结合,从图像上看反正弦函数的性 质 ()()1 f f x x x A -??=∈??()()1f f x x x D -=∈???? 三.例题与练习 例1 求值: (1);(2)()arcsin 1- ;(3)arcsin ? ?? (4)()arcsin 0.5;(5)arcsin0;(6)()arcsin 0.72-≈; (7)arcsin sin 9π?? ???;(8)5arcsin sin 6π?? ?? ? ; (8)()arcsin sin 3.49π 例2 用反正弦函数表示下列各式的: (1)sin x =,22x ππ?? ∈-???? (ii)[]0,2x π∈ (2)1sin 4x =-, (i),22x ππ?? ∈-???? (ii)[]0,2x π∈ (3)sin x =,22x ππ?? ∈-???? (ii)[]0,2x π∈ 例3 求下列函数的定义域和值域: (1)()3arcsin 21y x =- ;(2)6 y π =+ y =-. 四.布置作业 注意的不同范围 ()arcsin y f x =???? ()f x 定义域为A , 由()11f x -≤≤得 B ,则D A B = x x 三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值 2. 角度制与弧度制 设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°) 角度与弧度的换算 ①360°=2π rad ②1°=π/180rad ③1 rad=180°/π=57° 18′≈57.3° 弧长公式 l a R = 扇形的面积公式 12 s lR = 3. 诱导公式:(奇变偶不变,符号看象限) 所谓奇偶指是整数k 的奇偶性(k ·π/2+a ) 所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注: ①:诱导公式应用原则:负化正、大化小,化到锐角为终了 4. 三角函数的图像和性质:(其中z k ∈) ①: 三角函数 x y sin = x y cos = x y tan = cot y x = 函 数 图 象 定义域 R R 2 x k π π≠+ x k π ≠ 值域 [-1,1] [-1,1] R R 周期 2π 2π π π 奇偶性 奇 偶 奇 非奇非偶 单 调 性 2,222k k ππππ? ?-+↑????2,222k k ππππ??-+↑???? []2,2k k πππ-↑ []2,2k k πππ+↓ ,22k k ππππ? ?-+↑???? [],k k πππ+↓ 对 称 性 :2 x k π π=+ 对称轴 对称中心:(,0)k π :x k π =对称轴 : 对称中心(+ ,0) 2k π π : 对称中心( ,0)2 k π 零值点 πk x = 2 π π+ =k x πk x = 2 π π+ =k x 最 值 点 2 π π+ =k x ,1max =y 2 π π- =k x ,1min -=y πk x 2=,1max =y ; 2y k ππ=+,1min -=y 三角函数 1.特殊锐角( 0°, 30°, 45°, 60°, 90°)的三角函数值 2.角度制与弧度制 设扇形的弧长为l ,圆心角为 a (rad ), 半径为 R,面积为 S 角a 的弧度数公式2π×(a /360 °) ①360°=2π rad 角度与弧度的换算②1°=π/180rad ③1 rad= 180°/π=57° 18′≈ 57.3 ° 弧长公式l a R 扇形的面积公式s1lR 2 3.诱导公式:(奇变偶不变,符号看象限)所谓 奇偶指是整数 k 的奇偶性( k· /2+ a) 所谓符号看象限是看原函数的象限(将a 看做锐角, k· /2+ a 之和所在象限)注: ①:诱导公式应用原则:负化正、大化小,化到锐角为终了 学习指导参考 4. 三角函数的图像和性质: (其中 k z ) ①: 三角 函数 函 数 图 象 定义域 值域 周期 奇偶性 单 调 性 对 称 y sin x R [-1,1] 2 奇 2k , 2k 2 2 2k , 2k 2 2 对称轴 : x k 2 y cosx R [-1,1] 2 偶 2k ,2 k 2k ,2 k 对称轴 : x k y tanx y cotx x k x k 2 R R 奇 非奇非偶 k , k k , k 2 2 对称中心: ( k 2 , 0) 性 对称中心 : ( k , 0) 对称中心 : ( k + 2 , 0) 零值点 x k x k 2 最 x k , y max 1 x 2k , y max 1 ; 2 值 x k , y min 1 y 2k , y min 1 x k x 2 k 反三角函数 分类 反正弦 反余弦 余弦函数x y cos =在]0[π,上的反函数,叫做反余弦函数。记作x cos arc ,表示一个 余弦值为x 的角,该角的范围在]0[π,区间内。定义域]11[, - , 值域]0[π,。 反正切 反余切 余切函数y=cot x 在)0(π,上的反函数,叫做反余切函数。记作x arc cot ,表示一个余切值为x 的角,该角的范围在)0(π,区间内。定义域R ,值域)0(π,。 反正割 反余割 运算公式 余角关系 2 arccos sin arc π = +x x 2 cot tan arc π =+x arc x 2 csc ec a π = +x arc x rcs 负数关系 x x sin arc )sin(arc -=- x x rc arccos )cos(a -=-π x x tan arc )tan(arc -=- x rc x c cot a )(ot arc -=-π x rc x sec a )(arcsec -=-π x arc x c sec )(sc arc -=- 倒数关系 x arc x csc )1 arcsin(= x arc x sec )1 arccos(= x arc x arc x cot 2cot )1arctan(-==π x x x arc arctan 23arctan )1cot(-=+=ππ x x arc arccos )1 sec(= x x arc arcsin )1 csc(= 三角函数关系 加减法公式 1. ) 10,0()11arcsin(arcsin arcsin ) 10,0()11arcsin(arcsin arcsin ) 10()11arcsin(arcsin arcsin 22222 2 222222>+<<-+---=+>+>>-+--=+≤+≤-+-=+y x y x x y y x y x y x y x x y y x y x y x xy x y y x y x ,,或ππ 2. ) 10,0()11arcsin(arcsin arcsin ) 10,0()11arcsin(arcsin arcsin ) 10()11arcsin(arcsin arcsin 22222 2 222222>+><-----=->+<>----=-≤+≥---=-y x y x x y y x y x y x y x x y y x y x y x xy x y y x y x ,,或ππ 3. ) 0() 11arccos(2arccos arccos ) 0() 11arccos(arccos arccos 2 2 22<+----=+≥+---=+y x x y xy y x y x x y xy y x π 4. ) () 11arccos(arccos arccos ) () 11arccos(arccos arccos 2 2 22y x x y xy y x y x x y xy y x <--+=-≥--+-=- 5. ) 1,0(1arctan arctan arctan ) 1,0(1arctan arctan arctan ) 1(1arctan arctan arctan ><-++-=+>>-++=+<-+=+xy x xy y x y x xy x xy y x y x xy xy y x y x ππ 反三角函数的图像和性质 yx,arccos yx,arctanyx,arcsin ,1,1,1,1,,,,R 定义域 ,,,,,,,, ,,,,值域 [0,π] ,,,,2222,,,, 在上单调递增在上单调递减 ,1,1,1,1,,,,在R上单调递增单调性 无减区间无减区间无增区间 3奇偶性奇函数非奇非偶函数奇函数 32, 32,,21212,-1 图象 -22468-224682O11 -1,-1-,2-2 -22468-1 -1O2-2 -1 arcsin()arcsin,,,xxarccos()arccos,,,xx,arctan()arctan,,,xx 运算公x,,[1,1]x,,[1,1] xR,式1 运算公,,,, arccos(cos),[0,]xxx,,, arctan(tan),(,)xxx,,,arcsin(sin),[,]xxx,,,2222式2 运算公 sin(arcsin),[1,1]xxx,,,cos(arccos),[1,1]xxx,,,tan(arctan),xxxR,, 式3 , arctancotxarcx,,运算公,2 arcsinarccos,[1,1]xxx,,,,2式4 xR, 三角函数的图像和性质 4 yx,cosy,tanx yx,sin kZ,343 3222 1一个周11(((113,,2,,,期的图-22468,-22468(-4-2246823,,O,2,O2O--12-12-1-1-1 22像 -2-2 -2 -3,,,x|x,k,,k,Z ,定义域 R R ,,2,, [1,1],[1,1], 值域 R 奇偶性奇函数偶函数奇函数 , 2,2,周期 对 ,直线xk,kZ, ,,,称直线,无 xk,,kZ,2 轴对 称对 性称k,,(,0)k,,kZ, 点,kZ, 点(,0)k,(,0)点,kZ, ,22中 心 ,,,,,在上 [2,2]kk,,[2,22]kk,,,,,,,,,上在,上在(,)kk,,,,2222单调性 ,,3,在上,,[2,2]kk,,,,,[2,2]kk,,在上无减区间 22 反三角函数的概念和性质 . 一.基础知识自测题: 1.函数y=arcsin x的定义域是 [-1, 1] ,值域是. 2.函数y=arccos x的定义域是 [-1, 1] ,值域是 [0, π] . 3.函数y=arctg x的定义域是R,值域是. 4.函数y=arcctg x的定义域是R,值域是 (0, π) . 5.arcsin(-)=; arccos(-)=; arctg(-1)=; arcctg(-)=. 6.sin(arccos)=; ctg[arcsin(-)]=; tg(arctg)=; cos(arcctg)=. 7.若cos x=-, x∈(, π),则x=. 8.若sin x=-, x∈(-, 0),则x=. 9.若3ctg x+1=0, x∈(0, π),则x=. 二.基本要求: 1.正确理解反三角函数的定义,把握三角函数与反三角函数的之间的反函数关系; 2.掌握反三角函数的定义域和值域,y=arcsin x, x∈[-1, 1], y∈[-,], y= arccos x, x∈[-1, 1], y∈[0, π], 在反三角函数中,定义域和值域的作用更为明显,在研究问题时,一定要先看清楚变量的取值范围; 3.符号arcsin x可以理解为[-,]上的一个角或弧,也可以理解为区间[-,] 上的一个实数;同样符号arccos x可以理解为[0,π]上的一个角或弧,也可以理解为区间[0,π]上的一个实数; 4.y=arcsin x等价于sin y=x, y∈[-,], y=arccos x等价于cos y=x, x∈[0, π], 这两个等价关系是解反三角函数问题的主要依据; 5.注意恒等式sin(arcsin x)=x, x∈[-1, 1] , cos(arccos x)=x, x∈[-1, 1], arcsin(sin x)=x, x∈[-,], arccos(cos x)=x, x∈[0, π]的运用的条件; 6.掌握反三角函数的奇偶性、增减性的判断,大多数情况下,可以与相应的三角函数的图象及性质结合起来理解和应用; 7.注意恒等式arcsin x+arccos x=, arctg x+arcctg x=的应用。 例一.下列各式中成立的是(C)。 (A)arcctg(-1)=-(B)arccos(-)=- (C)sin[arcsin(-)]=-(D)arctg(tgπ)=π 解:(A)(B)中都是值域出现了问题,即arcctg(-1)∈(0, π), arccos(-)∈[0, π], (D)中,arctg(tgπ)∈[-, ], 而π[-,], ∴ (A)(B)(D)都不正确。 y=arcs inx. 函数y=sinx , x€ [- n /2 , n /2]的反函数叫做反正弦函数,记作x=arcsiny. 习惯上用x表示自变量,用y表示函数,所以反正弦函数写成y=arcsinx.的形式 请注意正弦函数y=sinx,x € R因为在整个定义域上没有一一对应关系,所以不存在反函数。 反正弦函数只对这样一个函数y=sinx , x€ [- n /2 , n /2]成立,这里截取的是正弦函数靠近原点的一个单调区间,叫做正弦函数的主值区间。 理解函数y=arcsinx中,y表示的是一个弧度制的角,自变量x是一个正弦值。这点必须牢记 性质 根据反函数的性质,易得函数y=arcsinx的,定义域[-1 , 1],值域[-n /2 , n /2],是单调递增函数 图像关于原点对称,是奇函数 所以有arcsin(-x)=-arcsinx ,注意x的取值范围:x € [-1 , 1] 导函数: arcsinx = (土匚(-1,1)) vl-x2,导函数不能取|x|=1 * / fim (arcsinx) =-oo lim {arcsinx) = +oo - . ,:T 1 反正弦恒等式 sin(arcsinx)=x , x € [-1 , 1] (arcsinx)'=1/ V (1-x A2) arcsin x=-arcs in(-x) arcs in ( sin x)=x , x 属于[0, n /2] arccosx 反三角函数中的反余弦。意思为:余弦的反函数,函数为y=arccosx,函数图像如右下图。 就是已知余弦数值,反求角度,如cos(a) = b,贝U arccos(b) = a ; 它的值是以弧度表达的角度。定义域:【-1 , 1】。 由于是多值函数,往往取它的单值支,值域为【0, n ],记作y=arccosx,我们称它叫 做反三角函数中的反余弦函数的主值, arcta n x 反三角函数中的反正切。意思为:tan(a) = b;等价于arctan(b) = a fflil 定义域:{x lx € R},值域:y € (- n/2,冗/2) 计算性质: tan( arcta na)=a arcta n(-x)=-arcta nx arctan A + arctan B=arcta n(A+B)/(1-AB) arctan A - arctan B=arcta n(A-B)/(1+AB) 反三角函数在无穷小替换公式中的应用:当x T 0时,arctanx~x 三角函数公式和图象总结 1.与角α终边相同的角,连同角α在内,都可以表示为S={β|β=α+k ×360,k ∈Z} 2.弧长公式:α?=r l 扇形面积公式lR S 21 = 其中l 是扇形弧长,R 是圆的半径。 3.三角函数定义: sin ,cos ,tan y x y r r x ααα===,其中P (,)x y 是α终边上一点,||r OP = 4.同角三角函数的两个基本关系式 22 sin sin cos 1 tan cos ααααα +== sin sin αsin β tan tan α sin cos), a x b x x? +=+其中tan b a ?=,?所在的象限与点(,) a b所在的象限一 致。 12.①sin()(0)y A x b A ω?=++>、cos()(0)y A x b A ω?=++>的最小正周期为 || ω,最大值为A+b ,最小值为-A+b. ②tan()(0)y A x b A ω?=++>的最小正周期为|| π ω 13.正弦定理: A a sin = B b sin =C c sin = 2R (R 为三角形外接圆半径) 14.余弦定理:2 2 2 2cos a b c bc A =+- bc a c b A 2cos 2 22-+= 15.S ⊿= 21a a h ?=21ab C sin =21bc A sin =2 1ac B sin =R abc 4=2R 2 A sin B sin C sin =))()((c p b p a p p ---(其中)(2 1 c b a p ++=, r 为三角形内切圆半径) 反三角函数图像与反三角函数特征 反正弦曲线 反余弦曲线 拐点(同曲线对称中心):,该点切线斜率为1 拐点 标准实用 反三角函数及最简三角方程 一、知识回顾: 1、反三角函数: 概念:把正弦函数y sin x , x,时的反函数,成为反正弦函数,记作 22 y arcsin x . y sin x( x R) ,不存在反函数. 含义: arcsin x 表示一个角;角,;sin x . 22 反余弦、反正切函数同理,性质如下表. 名称函数式定义域值域奇偶性单调性 反正弦函数y arcsin x1,1 增, 2奇函数增函数 2 y arccosx arccos( x)arccosx 反余弦函数1,1 减0,减函数 非奇非偶 反正切函数y arctanx R增, 2奇函数增函数 2 y arc cot x arc cot( x)arc cot x 反余切函数R减0,减函数 非奇非偶 其中: ().符号 arcsin x 可以理解为-, ] 上的一个角弧度,也可以理解为 1[ 2 () 2 区间[- , ] 上的一个实数;同样符号 arccos x 可以理解为 [0 ,π 上的一个角2 ] 2 (弧度 ),也可以理解为区间 [0 ,π]上的一个实数; (2). y =arcsin x 等价于 sin y=x, y∈ [-,], y= arccos x 等价于 cos y 22 =x, x ∈[0, π], 这两个等价关系是解反三角函数问题的主要依据; (3).恒等式 sin(arcsin x)=x, x∈ [- 1, 1] , cos(arccos x)=x, x∈ [-1, 1], tan(arctanx)=x,x ∈ R arcsin(sin x) = x, x ∈ [ -,], arccos(cos x) = x, x ∈ [0, 22 π],arctan(tanx)=x, x∈(-,)的运用的条件; 22 (4).恒等式 arcsin x+arccos x=, arctan x+arccot x=的应用。 22 2、最简单的三角方程 方程方程的解集 a1x | x2k arcsin a, k Z sin x a a1x | x k 1 k arcsin a, k Z a1x | x2k arccos a, k Z cos x a a1x | x2k arccos a, k Z tan x a x | x k arctana, k Z cot x a x | x k arc cot a, k Z 其中: (1 ).含有未知数的三角函数的方程叫做三角方程。解三角方程就是确定三 角方程是否有解,如果有解,求出三角方程的解集; (2).解最简单的三角方程是解简单的三角方程的基础,要在理解三角方程的 三角、反三角函数图像 (附:资料全部来自网络,仅对排版做了改动,以方便打印及翻阅,其中可能出现错误,阅者请自行注意。) 1.六个三角函数值在每个象限的符号: sinα·cscα cosα·secα tanα·cotα 2.三角函数的图像和性质: 1-1y=sinx -3π2 -5π2 -7π2 7π2 5π 2 3π2 π2 -π2 -4π-3π -2π4π 3π 2ππ -π o y x 1-1y=cosx -3π 2 -5π2 -7π 2 7π2 5π2 3π2 π2 -π2 -4π-3π-2π4π 3π 2π π -π o y x y=tanx 3π2 π π2 - 3π2 -π - π2 o y x y=cotx 3π2 π π2 2π -π - π2 o y x 函数 y=sinx y=cosx y=tanx y=cotx 定义域 R R {x |x∈R 且x≠kπ+2 π ,k∈Z } {x |x∈R 且x≠kπ,k∈Z} 值域 [-1,1]x=2kπ+ 2 π 时y max =1 x=2kπ-2 π 时y min =-1 [-1,1] x=2kπ时y max =1 x=2kπ+π时y min =-1 R 无最大值 无最小值 R 无最大值 无最小值 周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性 奇函数 偶函数 奇函数 奇函数 单调性 在 [2kπ- 2 π ,2kπ+ 2 π ] 上都是增函数;在 [2kπ+ 2 π ,2kπ+ 3 2 π]上都是减函数 (k∈Z) 在[2kπ -π, 2kπ]上都是增 函数;在[2kπ, 2kπ+π]上都是 减函数(k∈Z) 在(kπ- 2 π , kπ+ 2 π )内都是 增函数(k∈Z) 在(kπ,kπ+π) 内都是减函数 (k∈Z) 3.反三角函数的图像和性质: arcsinx arccosx arctanx arccotx 名称反正弦函数反余弦函数反正切函数反余切函数 定义 y=sinx(x∈ 〔- 2 π , 2 π 〕的反 函数,叫做反正弦 函数,记作 x=arsiny y=cosx(x∈ 〔0,π〕)的反函 数,叫做反余弦 函数,记作 x=arccosy y=tanx(x∈(- 2 π , 2 π )的反函数,叫 做反正切函数,记作 x=arctany y=cotx(x∈(0, π))的反函数, 叫做反余切函 数,记作 x=arccoty 理解 arcsinx表示属于 [- 2 π , 2 π ] 且正弦值等于x的 角 arccosx表示属 于[0,π],且 余弦值等于x的 角 arctanx表示属于 (- 2 π , 2 π ),且正切 值等于x的角 arccotx表示属 于(0,π)且余切 值等于x的角 性 质 定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞) 值域[- 2 π , 2 π ][0,π](- 2 π , 2 π )(0,π)单调性 在〔-1,1〕上是增 函数 在[-1,1]上是 减函数 在(-∞,+∞)上是增 数 在(-∞,+∞)上 是减函数 三角函数及反三角函数集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988) 函数变换 反三角函数 三角函数的,是多值函数。它们是反正弦Arcsin x,反余弦Arccos x,反正切Arctan x,反余切Arccot x等,各自表示其正弦、余弦、正切、余切、正割、余割为x的角。为限制为单值函数,将反正弦函数的值y限在y=-π/2≤y≤π/2,将y为反正弦函数的主值,记为y=arcsin x;相应地,反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2 例 试判断下列函数的定义域、值域、奇偶性、周期性、单调性,并画出大致图像。 (1)()sin arcsin y x =。 (2)()arcsin sin y x =。 解:(1)()()sin arcsin y f x x x ===。 定义域为[]1,1-。值域为[]1,1-。奇函数。 ()f x 不是周期函数,且再[]1,1-上单调递增,如图。 (2)()()arcsin sin y f x x ==。 定义域为R 。值域为,22ππ?? -????。奇函数。 ()f x 是周期函数,周期为2π。 下面讨论单调性: ① 当,22x ππ?? ∈- ???? 时,()()arcsin sin f x x x ==,为增函数。 ② 当3,22x ππ?? ∈? ??? 时,()()()arcsin sin arcsin sin f x x x x ππ==-=-????,为减函数。 由函数的周期性,得 ① 区间2,22 2k k π πππ?? - + ??? ? (k Z ∈)为函数()f x 的递增区间,此时 ()()()arcsin sin arcsin sin 22f x x x k x k ππ==-=-????,k Z ∈。 ② 区间32,22 2k k π πππ? ? + + ??? ? (k Z ∈)为函数()f x 的递减区间,此时 ()()()arcsin sin arcsin sin 22f x x k x k x ππππ==+-=+-????,k Z ∈。 所以()2,2,222arcsin sin 32,2,222x k x k k y x k x x k k πππππππππππ???-∈-+????? ?==??? ?+-∈++?????? ,k Z ∈。如图。 反三角函数的概念和性质 反三角函数的概念和性质 一.基本知识: 1.正确理解反三角函数的定义,把握三角函数与反三角函数的之间的反函数关系; 2.掌握反三角函数的定义域和值域,y=arcsin x, x∈[-1, 1], y∈[-,], y=arccos x, x∈[-1, 1], y∈[0, π], 在反三角函数中,定义域和值域的作用更为明显,在研究问题时,一定要先看清楚变量的取值范围; 3.符号arcsin x可以理解为[-,]上的一个角或弧,也可以理解为区间[-,]上的一个实数;同样符号arccos x可以理解为[0,π]上的一个角或弧,也可以理解为区间[0,π]上的一个实数; 4.y=arcsin x等价于sin y=x, y∈[-,], y=arccos x等价于cos y=x, x∈[0, π], 这两个等价关系是解反三角函数问题的主要依据; 1)∈(0, π), arccos(-)∈[0, π], (D)中,arctg(tgπ)∈[-, ], 而π[- ,], ∴ (A)(B)(D)都不正确。 例二.下列函数中,存在反函数的是(D)。 (A)y=sin x, x∈[-π, 0](B)y=sin x, x∈[, ] (C)y=sin x, x∈[,] (D)y=sin x, x∈[,] 解:本题是判断函数y=sin x在哪个区间上是单调函数,由于y=sin x在区间[,]上是单调递减函数,所以选D。 例三. arcsin(sin10)等于(C)。 (A)2π-10 (B)10-2π(C)3π-10 (D)10-3π 解:本题是判断哪个角度的正弦值与sin10相三角函数,反三角函数公式大全
三角和反三角函数图像
反三角函数
三角和反三角函数图像
三角及反三角函数
常用反三角函数公式表
.反三角函数例题
三角函数和反三角函数图像性质知识点总结
三角函数与反三角函数图像性质、知识点总结
反三角函数公式(完整)
三角和反三角函数图像性质总结
反三角函数的概念和性质
反三角函数及性质
大学高数 函数与反三角函数图像
反三角函数及最简三角方程.docx
角、反三角函数图像及性质与三角公式
三角函数及反三角函数
反三角函数
反三角函数的概念和性质
